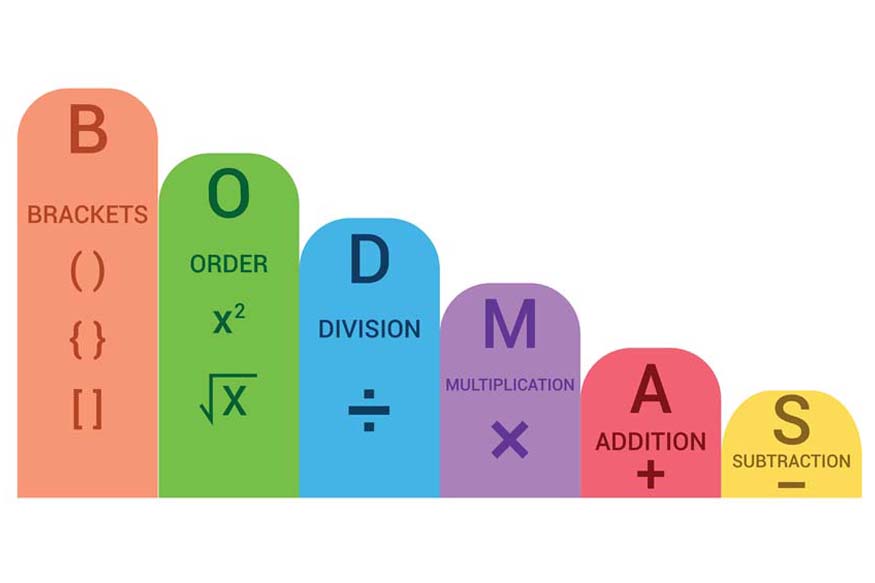
Mathematics can be challenging, especially when dealing with complex equations. However, rules like BODMAS offer a clear, step-by-step method to simplify these equations. BODMAS stands for Brackets, Orders (i.e., powers and roots), Division, Multiplication, Addition, and Subtraction. Following this order ensures consistency and correctness in solving mathematical problems.
Understanding BODMAS
What is the BODMAS rule?
The BODMAS rule, known as the order of operations, provides a systematic approach for executing calculations in arithmetic expressions. Mathematics relies heavily on logic and established guidelines that facilitate our computations. Consequently, the BODMAS rule serves as one of the fundamental principles for simplifying expressions that contain various operators.
An arithmetic expression or equation has two main components:
- Numbers
- Operators
Numbers
Numbers are mathematical elements that are utilised for counting, quantifying, and performing calculations. In mathematics, they can be categorised into several types, including natural numbers, whole numbers, integers, rational numbers, irrational numbers, real numbers, complex numbers, and imaginary numbers.
Operators or Operations
An operator is a symbol that connects two numerical values to create an expression or equation. In mathematics, the primary operators include Addition (+), Subtraction (-), Multiplication (×), and Division (÷). When dealing with mathematical expressions or equations that involve only one operator, determining the result is relatively straightforward. However, when multiple operators are present, the process of finding a solution can become more complex. To illustrate this, consider the example where person A and person B each solved the expression 6 × 3 + 2 separately. Below are the distinct approaches they used to arrive at their solutions.
Person A’s Method: 6 × 3 + 2 = 6 × 5 = 30, and
Person B’s Method: 6 × 3 + 2 = 18 + 2 = 20.
As we can observe, person A and person B got different answers.
In mathematics, there can only be one correct answer to this expression. So, how do you decide who is correct?
This is where the BODMAS rule comes into the picture.
The BODMAS rule outlines the order of operations to be followed when simplifying an expression. BODAMS rule full form is as follows –
Brackets (B): Solve expressions within parentheses or brackets first.
Orders (O): Evaluating exponential components (powers and roots, etc.).
Division (D) and Multiplication (M): Perform division and multiplication from left to right.
Addition (A) and Subtraction (S): Lastly, perform addition and subtraction from left to right.
Why is BODMAS Important?
|
B |
[{( )}] |
Brackets |
|
O |
x² |
Order of Powers or Roots (in some cases, ‘of’) |
|
D |
÷ |
Division |
|
M |
× |
Multiplication |
|
A |
+ |
Addition |
|
S |
– |
Subtraction |
The significance of the BODMAS rule lies in its ability to prevent errors. Without following this order, different people might interpret and solve the same equation differently, leading to incorrect results. BODMAS standardises the process, ensuring everyone arrives at the correct answer.
So, how do you apply this BODMAS rule?
Breaking Down BODMAS with Examples
Example 1: Basic Application
Consider the expression:
7+3×2
According to BODMAS:
Multiplication before Addition:
3×2=6
So the expression simplifies to:
7+6=13
Example 2: Incorporating Brackets
Now, look at:
(8−2)×3
First, solve inside the brackets:
8−2=6
Then, multiply:
6×3=18
Simplification using the BODMAS rule
Example 3: Including Orders
Let’s take:
5+23÷4
First, handle the exponent (Order):
23=8
Next, divide:
8÷4=2
Finally, add:
5+2=7
Example 4: More Complex Equations
Consider a more complex expression:
12÷(2+2)×32−4
Following BODMAS:
Brackets: Solve inside the brackets first:
2+2=4
So, the expression becomes:
12÷4×32−4
Orders: Evaluate the exponent:
32=9
The expression now is:
12÷4×9−4
Division and Multiplication: Process from left to right:
12÷4=3
and
3×9=27
The expression is now:
27−4
Addition and Subtraction: Finally, subtract:
27−4=23
Now that we have learned about BODMAS, let us understand another similar rule.
BODMAS or PEMDAS

BODMAS and PEMDAS are two acronyms that help in identifying the order of operations in mathematics. The BODMAS rule closely resembles the PEMDAS rule, with variations in the abbreviation reflecting different terminologies used in various countries. When applying either the BODMAS or PEMDAS rule, it is important to note that for division and multiplication, the operation that appears first from the left side of the expression should be performed first. This same principle applies to addition and subtraction, where the operation that comes first on the left side is prioritised.
Common Errors While Using the BODMAS Rule
Errors that commonly arise when applying the BODMAS rule to simplify expressions, as outlined below:
- The presence of multiple brackets can lead to confusion, potentially resulting in incorrect answers. To avoid this, it is advised to solve all identical types of brackets simultaneously when they appear in an expression.
- Misunderstandings regarding the addition and subtraction of integers can lead to mistakes. For instance, while 2-4+5 simplifies correctly to -2+5=3, errors may occur, such as incorrectly calculating 2-4+5 as 2-9=-7.
- A common misconception is that division takes precedence over multiplication and that addition is prioritised over subtraction. Adhering to the left-to-right rule when performing these operations is essential for obtaining the correct result.
- Both multiplication and division are operations of equal importance and should be executed in the order they appear from left to right. Similarly, addition and subtraction are equal-level operations that should be performed after addressing multiplication and division. If division is mistakenly performed before multiplication, despite multiplication appearing first in the expression, it can lead to an incorrect outcome.
Conclusion
Mastering the BODMAS rule is essential for anyone tackling mathematical equations, from basic arithmetic to more complex algebraic expressions. By following this rule, you ensure accuracy and consistency in your calculations. Regular practice will make using BODMAS second nature, simplifying your approach to solving equations.
For more such informative/interesting blogs, visit Center Point School.