Trigonometry is a part of math that focuses on triangles and circular shapes. Trigonometric functions help explain the characteristics of angles, the connections in triangles, and the patterns of repeating cycles. By learning trigonometry, you can better visualise and graph these relationships and cycles.
Before diving into the more complex aspects of trigonometry, it is essential to have a strong grasp of the basics. This includes understanding what trigonometry is and its importance. Trigonometry is primarily concerned with right-angled triangles, but it is principles can be extended to other types of triangles and periodic functions. The fundamental concepts include angles, sides, and the relationships between them.
Key concepts of trigonometry
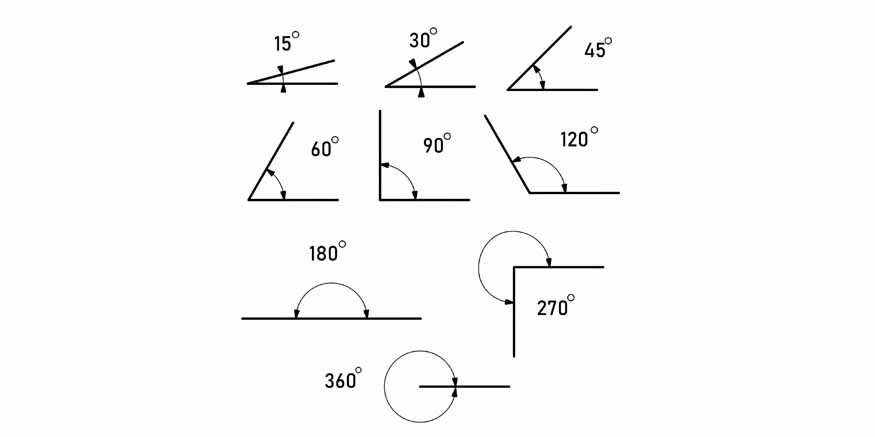
- Angles and their Measurement: Angles can be expressed in degrees or radians. A complete circle measures 360 degrees or 2π radians. It is important to know how to switch between these two measurement systems.
- Right-Angled Triangles: The foundation of trigonometry lies in right-angled triangles, which have one angle that is exactly 90 degrees. The side opposite the right angle is called the hypotenuse, while the other two sides are referred to as the adjacent and opposite sides about a specific angle.
- Sine, Cosine, and Tangent: These are the main trigonometric functions that connect the angles to the sides of a right-angled triangle. The sine (sin) of an angle is found by taking the ratio of the length of the opposite side to that of the hypotenuse. The cosine (cos) of an angle is determined by the ratio of the length of the adjacent side to the hypotenuse. The tangent (tan) of an angle is the ratio of the length of the opposite side to the length of the adjacent side.
- The Unit Circle: A unit circle is defined as a circle with a radius of one, positioned at the origin of a coordinate system. It serves as an essential tool for grasping how trigonometric functions apply not just to right-angled triangles but to any angle as well.
Basic Trigonometry Formulas
Knowing the basic trigonometry formulas is essential for solving problems and understanding more complex trigonometry concepts. Here are some fundamental formulas:
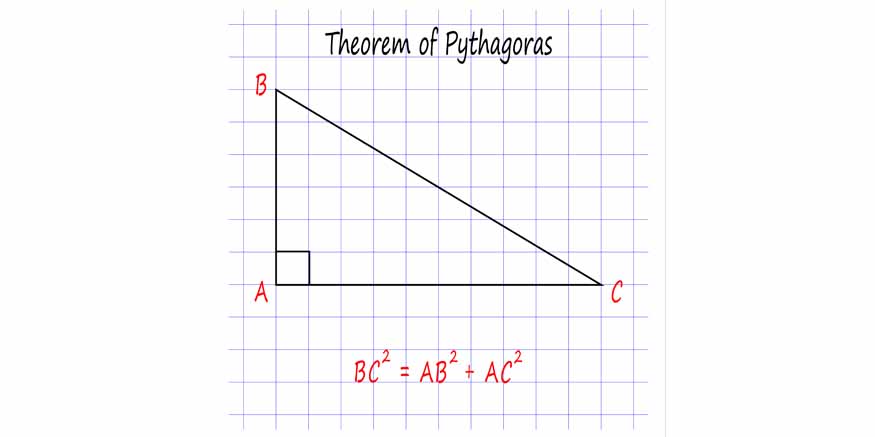
- Pythagorean Theorem: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
- Sine, Cosine and Tangent Identities:
- Reciprocal identities
- Pythagorean identities
- Trigonometry in flight engineers: Aviation and flight engineering have advanced applications in trigonometry. This math helps figure out how fast an aeroplane is going, which way it is headed, and how far it can travel. It also takes into account the wind’s speed and direction, which is super important for takeoffs and landings. Knowing the right angle and speed to use during these times can make a big difference for the aircraft.
- Trigonometry in Navigation: Navigation is another area with vast applications of trigonometry. Trigonometric functions are really useful here because they make it easier to determine where you are and how far away you are from your goal. Additionally, satellite navigation systems rely on trigonometric functions, like the law of cosines, to solve equations that help track satellites orbiting the Earth around the clock.
- Trigonometry in Measuring Heights: Calculating the height of a mountain or a tall building is made pretty simple using trigonometry. To find the height, you just need to measure how far you are from the base and then figure out the angle of elevation to the top. This creates a right triangle with three sides: the height, the distance from the base, and the hypotenuse. These three elements are essential for solving any trigonometric problems.
c2 = a2+ b2
Sin(θ) =
Cos(θ)=
Tan(θ) =
Cosec(θ)=
Sec(θ)=
Cot(θ)=
sin2(θ) + cos2(θ)=1
1 + tan2(θ)= sec2(θ)
1 + cot2(θ) = cosec2(θ)
Applications of Trigonometry
For example, imagine a boy standing next to a tree, looking up and thinking, “How tall is that tree?” You can find out the height without actually measuring it directly. In this case, we have a right triangle, which has one angle that is 90 degrees. By using trigonometric formulas, you can calculate the height of the tree if you know the distance from the boy to the tree and the angle he sees it from the ground.
The tangent function helps us figure this out. The tangent of an angle is the ratio of the tree’s height to the distance from the tree. If we call the angle θ, then we can express it like that.
tan θ =
distance=
Let us assume that the distance is 30m and the angle formed is 45 degrees, then
height=
tan45°= 1
height= 30m
The height of the tree can be found out by using basic trigonometry formulas.
Understanding trigonometry concepts is crucial for success in advanced mathematics and various scientific fields. By mastering the basic trigonometry formulas and exploring the application of trigonometry in real-world contexts, students can develop a solid foundation in this essential branch of mathematics. Regular practice, visual aids, and a deep understanding of the theory can make learning trigonometry more manageable and enjoyable.
At Center Point School, we strive to provide students with the skills and knowledge they need to excel in trigonometry and beyond. Our commitment to fostering a supportive and enriching learning environment ensures that students not only grasp these vital concepts but also appreciate their real-world applications. Through our comprehensive approach, we aim to inspire confidence and a passion for mathematics in every learner.